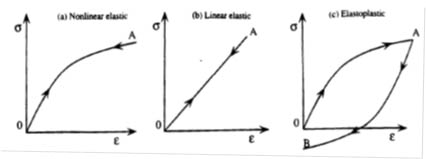
組成律模式為一個定義材料巨觀上應力應變關係的模型。最簡單的例子為線性彈性模型(Linearly Elastic),只需要兩個參數即可(譬如說,Young's Modulus 與 Poisson's Ratio)。其應力的增量與應變的增量成一個固定的比例。在大學部的土壤力學裡,計算土體地表受荷載所導致的應力增量,即假設土體為一個等向均質的線性彈性體。當考慮土壤的沉積或岩體的層理時,我們可以使用橫向等向(Transversely Isotropic)的彈性模型。從野外所取得的土樣或岩心試體,可以透過不同方向的壓縮試驗,反算此試體的異向性(Anisotropy),以決定沉積面或層理面的走向(Orientation)。在運用極限平衡法(Limit Equivalent Method)計算邊坡的滑動時,我們假設沿著破壞面(Slip Surface)的土壤是處於一個完全塑性(Perfectly Plastic)的狀態。另外,土壤壓密試驗所求得的壓縮指數(CC),也是一個組成律,用以計算土層受荷載的壓密沉陷。圖1為基本的應力應變曲線。
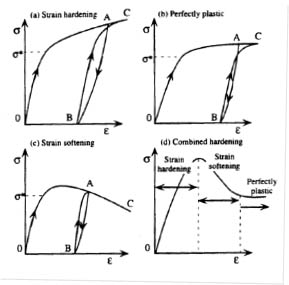
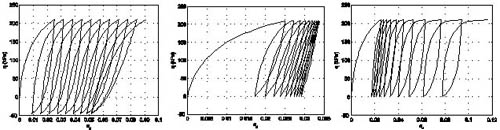
在使用有限元素法(Finite Element Method)或有限差分法(Finite Difference Method)解一個邊值問題(Boundary Value Problem)時,我們需要定義材料的組成律模式。如果用一個線性彈性的組成律時,我們稱之為線性有限元分析。若使用一個非線性的組成律時(譬如說,彈塑性模型),我們稱之為非線性有限元分析。當然,我們這裡所談的非線性是指材料的非線性(Material Nonlinearity)。幾何的非線性(Geometric Nonlinearity)在大地工程是比較少用到的,在此就不多做論述。想當然爾,如果我們使用的組成律能越真實地反映材料的行為,有限元素法的計算結果越能接近現場地工結構物的反應。正因如此,在有限元素法於1960年代末期開始迅速發展後,大地材料的組成律模式一直是個熱門的研究課題。尤其在土壤的非線性應力應變行為,極度非線性的剪脹(Shear-Dilantancy)行為,受循環荷載的Hysteresis Loops,主應力軸的旋轉(Principal Stress Rotation)問題以及土壤的液化(Soil Liquefaction)行為等,均有極大的進展。 英國劍橋大學的Cam Clay Model,為一個非常著名的彈塑性組成律。它只需要六個參數,就可在一個理論架構下,很有效地描述土壤在不同初始狀態下的應力、應變、強度行為。此理論架構稱為臨界土壤力學(Critical State Soil Mechanics)。在一般的彈塑性組成律裡,我們同時運用到彈性理論(Theory of Elasticity)與塑性理論(Theory of Plasticity)。塑性應變的增量,是由塑性流動準則(Plastic Flow Rule)所定義,其方向由塑性勢能函式(Plastic Potential)決定,而其量值需透過Consistency Condition決定。彈塑性在應力空間中是由降服函式(Yield Function)區隔。透過硬化準則(Hardening Rules),降服函式在應力空間中是可以變大(Isotropic Hardening)、變小(Isotropic Softening)、移動(Kinematic Hardening)、或轉動(Spinning Hardening)。圖2為具代表性的塑性硬化,軟化彈塑性模型應力應變曲線。以上討論的彈塑性組成律,無法有效地描述土壤受循環荷載下的行為,因此有循環塑性理論(Cyclic Plasticity Theory)的產生。Multi-Surface Plasticity,Bounding Surface Plasticity,Generalized Plasticity,以及Fuzzy Set Plasticity為具代表性的組成律(圖3)。
材料的異向性為另一個重要的考慮。異向性主要可分為兩類,一為固有異向性(Inherent Anisotropy),另一為應力導致的異向性(Stress-Induced Anisotropy)。彈塑性組成律多少可以描述應力導致的異向性,但要描述固有異向性,必須引進一個新的參數叫結構張量(Fabric Tensor)。不然,可以使用另一種類別的組成律,來描述材料初始的方向性。此類組成律以Microplane Model與Multi-Laminate Model為代表。 由於岩體包含了不連續面(Discontinuity),這些不連續面在做有限元或有限差分時要另做處理。通常我們可以使用界面元素(Interface Element)來達成此目的。當然,我們也可以把岩體裡的不連續面與完整的岩塊(Intact Rock)做同質化等效處理(Homogenization)。離散元素法(Distinct/Discrete Element Method)為近來頗受歡迎的分析方法。其組成律為定義顆粒間的正向彈簧(Normal Stiffness)與剪力彈簧(Shear Stiffness)。顆粒間也允許鍵節以描述顆粒間的內凝聚力(Cohesion)。離散元素法的優點為可以探討較微觀的材料行為,但所需的計算時間遠比同規模的有限元要來的多,並且,其組成律的參數校正也相較困難許多。我們若往更微觀的方向看下去,分子動力分析(Dynamic Molecular Simulation)討論分子間的交互關係(Interaction)。其與離散元素法在某種層面類似,皆運用牛頓第二運動定律來計算顆粒間的交互關係,主要的不同之處,在於分子間的關係是透過萬有引力的勢能方程式所決定。目前在大地工程的應用還不多見。 由以上的討論我們可以看出,組成律模式實為邊值問題數值分析的核心。選取一個適當的組成律,將可更準確的分析或預測一個工程實務問題。一個好的組成律,不在於擁有眾多參數的組成律。一個能用越少的參數,有效地描述主要的力學行為,實為一個好的組成律。既使有一個好的組成律,並不表示所計算出來的結果是百分之百現場所發生的行為,因為,組成律畢竟是個模型。
|