杜風 102 期 特別報導 |
計算塑性力學的發展與願景
The development and prospect of computation plasticity
劉立偉
台灣大學土木工程學系博士 |
彈性組成模式並不足以描繪真實結構物與材料上所觀察到的力學行為,是眾所皆知的事實。故發展非彈性組成模式是必須的,而相關的計算丶分析與設計研究也是必要的。非彈性力學包含黏彈性力學、彈塑性力學與黏彈塑性力學等,這些都是為了描繪真實力學行為所發展出來的學問。其中塑性力學的理論內涵與其廣泛的實用性,深深吸引著筆者一頭栽進相關的研究中。
幾乎所有的塑性模式都可以整理成由「常微分方程組」 + 「代數等式與不等式」所組成的數學型式,其中常微分方程組描述了塑性時塑性應變率的變化與應力硬軟化的行為,而代數式與不等式則是規範應力可允許區域(降伏條件)丶耗散非負與彈塑切換機制。當塑性時,應力點根據常微分方程組與代數等式的規範,在降伏面上變化。此時降伏面可能是固定不動的,也可能是演化變動的。
正確求解塑性模式,在模式發展過程中的模式分析,與模式發展完成後隨之的應用,都是必須的。由於塑性模式的數學形式相當複雜,故使用解析的方式來求得模式的反應已不可行。
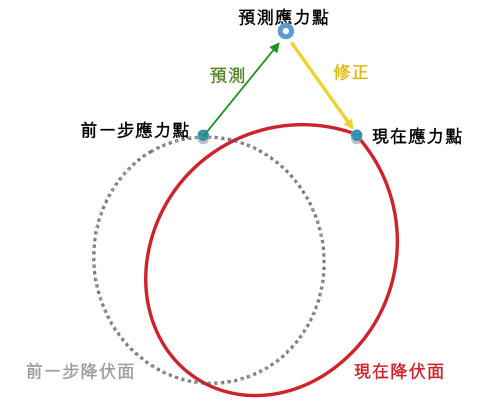 |
| Return mapping 法示意圖 |
求解能夠描述如此複雜行為的塑性模式,必須同時面對常微分方程組與代數等式與不等式的束制。單單僅求解常微分方程組,或僅求解代數等式與不等式是容易的,在數值方法上已發展出很好的方法:如Raunge-Kutta法可得到很高精度的常微分方程組數值解;而線性規劃、非線性規劃或數學規劃理論,則是針對代數等式與不等式提供系統性的數值求解。然而,求解塑力問題時,必須同時處理常微分方程組與代數等式與不等式,若僅使用求解常微分方程組的數值方法,則會造成所得之應力值在塑性時不滿足代數式束制,也就是應力點不在降伏面上。
Return mapping法
為了使應力點在塑性時位於降伏面上, Wilkins 首先針對具有 von Mises 降伏條件的完全彈塑性模式,提出著名的Return mapping法 — 結合彈性預測與塑性修正的數值求解彈塑性模式方法 [1]。在接下來的數十年,Return mapping法的應用與發展,除了持續針對完全彈塑性模式 [2],也被推廣到等向硬化彈塑性模式 [3]、黏塑性模式 [4] 與多種複雜的彈塑性模式 [5,6,7,8]。在這些應用推廣中,塑性修正的策略也因應模式的不同,制定出了 Radial return法丶 Mean normal 法與 Closest points 法等等。
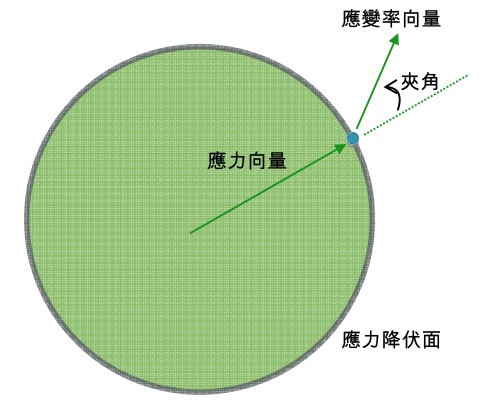 |
| Krieg-Krieg 法示意圖 (完全彈塑性模式,降伏面不動) |
除此之外,有鍳於彈性預測與塑性修正的計算效率不彰,學界也提出了塑性預測與彈性修正的算法 [9]。實際上,由於彈塑性模式的持續發展,針對不同光滑或非光滑降伏條件,與結合不同硬軟化彈塑性模式的各類先預測-後修正(或稱應力更新)數值方法,也陸續被提出 [10,11,12,13,14,15]。
然而,正如先前的研究指出,即使是簡單的完全彈塑性模式,Return mapping法的應力更新過程,需耗費大量的計算時間。若更進一步,考慮到3維固體在應力分析時,數以萬計的元素,都需要在每一個時間點執行應力更新。因此,耗時的應力更新過程,將會造成3維固體應力歷時分析花費巨大的計算時間,是否有任何方法能夠大幅改善應力更新的效率呢?
Angles based integrations
顯現大幅改進計算效率可能性的曙光,最先是在 Krieg and Krieg的論文中[2],他們針對具有von Mises降伏條件的完全彈塑性材料組成模式—即Prandtl-Reuss模式,觀察出偏差應力與偏差應變率所夾之夾角的變化規則,建立了規範夾角變化的微分方程式,更進一步解得夾角變化的解析解。
甚而,他們還定出「下一步徧差應力值」與「現在徧差應力值」丶「現在夾角值」與「下一步夾角值」的關係式 —「下一步徧差應力值公式」。由此關係式,無論是在任何的「現在夾角值」與「下一步夾角值」,所得到的「下一步徧差應力值」必定會滿足von Mises降伏條件,因此,下一步徧差應力值公式可保証,在塑性時應力點一定在降伏面上。
由於下一步徧差應力值公式為顯式,因此不需迭代,應力更新一步到位,這樣的優勢吸引著學界。所以即使夾角變化解析解僅可在Prandtl-Reuss模式得到,但引入夾角,並結合下一步徧差應力值公式的手法,還是不斷持續推廣到其他更複雜的彈塑模式: 如具有von Mises 降伏條件的線性等向硬化模式 [16]與線性等向走動硬化模式 [17], 具有Drucker-Prager 降伏條件的線性等向硬化模式[18]丶線性等向硬化與Armstrong-Frederick走動硬化模式 [19]、 Chaboche 等向走動硬化模式 [20];此方法也被推廣至求解彈塑性破壞模式[21]。
內在對稱性與保群算法
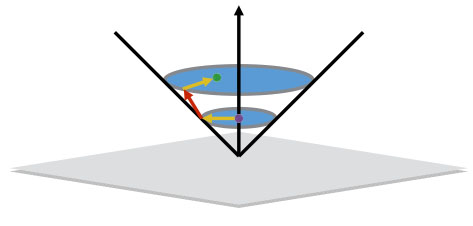 |
| 增廣應力閔氏時空示意圖 |
|
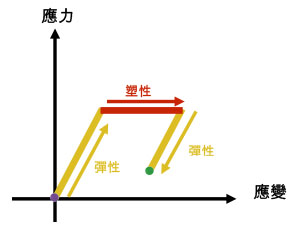 |
| 完全彈塑應力應變示意圖 |
|
真正的突破開始於發現了彈塑性模式的內在對稱性。完全彈塑性模式的內在結構首先被研究 [22,23,24,25,26]:引入一新變數並建立增廣力空間後,發現此響應空間竟為閔氏時空(Minkowski spacetime),而塑性時應力點在降伏面上演化的過程,在響應空間中則是顯現為光錐(Light cone)面上的運動,此運動軌跡則由勞倫茲群(Lorentz group) 規範。
應力點在應力空間中降伏面上演化,讓人能很自然地由微分流形(differentialbe manifold)與其李群變換(Lie group transformation),建立塑性力學的數學觀點。根據李群特性建構出的數值算法,能夠不經由修正,在塑性狀態下求得滿足von Mises降伏條件的應力值。
除了完全彈塑性模式,彈塑性線性/非線性走動硬軟化模式 [27,28,29]、缐性等向走動硬軟化損傷模式 [30,31]、Drucker-Prager降伏面完全彈塑性模式[32]與異向性降伏面完全彈塑性模式[33]的內在對稱性也接續被發現,並更進一步依據其對稱性建立數值算法。此種依據內在對稱性所建構出的計算方法被稱為保群算法(Group-preserving schemes)或保結構算法(Structure-preserving schemes)。
受彈塑性模式內在對稱性研究的啟發,學界針對具有von Mises 降伏面的線性等向走動硬化模式,發展出了Consistent exponential map[34,35],此數值算法,在塑性時,也可得到滿足降伏條件的應力值。接著,此算法也被推廣至Armstrong-Frederick走動硬化模式[36]與 Chaboche、Ohno-Wang或 Abdel-Karim-Ohno 走動硬化模式 [37]。雖然在上述著作中都未提及,但不可否認的事實是:Consistent exponential map法利用了李群的特性來建構算法,因此也屬於是保群算法的一種。
特別值得一提的是,上述各類保群算法,都是藉由引進新變數的手法,來建構增廣應力空間,進而探索出模式各自的內在對稱性,並發展其算法。儘管其它塑性模式的內在對稱性還未被發現,其塑性時的演化方程式,還是可以重新被建立在增廣應力空間上,並發展出Exponential-based算法[38,39,40,41,42,43,44]。
展望
至今,所發展出的塑性模式計算方法各有所長,Return mapping法針對大部分現存的模式,提供了一致的算則 — 先預測後修正。然而,其修正方法,則必須依照不同的模式來加以制定;而如前所述,修正過程非常耗時。另一方面,保群算法的建立,必須要針對各個模式,探索其內在對稱性;但現今已發現內在對稱性的模式數量仍相當少。
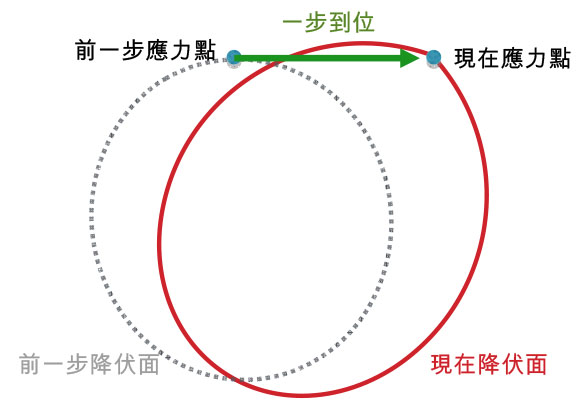 |
| 保群算法示意圖 |
再者,由於工程界與工業界的實用需求,固體的力學行為被研究的更加透徹,因此隨之發展出的塑性模式就更加複雜。然而,模式的複雜度越高,Return mapping法中的修正算則會越難以制定,且修正過程會越耗時;當然,要發掘出模式的內在對稱性更是難上加難。
倘若,有一個數學架構能夠持續發展新的模式,以滿足現今工程界與工業界的需求。而此數學架構中的模式,都具有相似的內在對稱性,進而可利用其內在對稱性,發展出不需修正過程,就可使塑性時每個應力點都在降伏面的數值方法。這樣的數學架構與兼具Return mapping法之廣泛性與保群算法之高效率的塑性模式計算方法是否為南柯一夢,值得學界與筆者深究之。
參考文獻
- M. L. Wilkins, Calculation of elastic-plastic flow, Methods of Computational Physics, Vol. 3, Academic Press, New York, 1964.
- R. D. Krieg, D. B. Krieg, Accuracies of numerical solution methods for the elastic-perfectly plastic model, Journal of Pressure Vessel Technology 99 (1977) 510–515.
- H. L. Schreyer, R. F. Kulak, J. M. Kramer, Accurate numerical solutions for elastic-plastic models, Journal of Pressure Vessel Technology 101 (1979) 226–
234.
- M. Ortiz, P. M. Pinsky, R. L. Taylor, Operator split methods for the numerical solution of the elastoplastic dynamic problem, Computer Methods in Applied Mechanics and Engineering 39 (1983) 137–157.
- M. Ortiz, E. P. Popov, Accuracy and stability of integration algorithms for elastoplastic constitutive relations, International Journal for Numerical Methods in Engineering 21 (1985) 1561–1576.
- J. Simo, R. Taylor, Consistent tangent operators for rate-independent elastoplasticity, Computer Methods in Applied Mechanics and Engineering 48 (1985) 101–118.
- M. Ortiz, J. C. Simo, An analysis of a new class of integration algorithms for elastoplastic constitutive relations, International Journal for Numerical Methods in Engineering 23 (1986) 353–366.
- M. Ortiz, J. B. Martin, Symmetry-preserving return mapping algorithms and incrementally extremal paths: A unification of concepts, International Journal for Numerical Methods in Engineering 28 (1989) 1839–1853.
- S. Nemat-Nasser, Rate-independent finite-deformation elastoplasticity: a new explicit constitutive algorithm, Mechanics of Materials 11 (1991) 235–249.
- O. S. Hopperstad, S. Remseth, A return mapping algorithm for a class of cyclic plasticity models, International Journal for Numerical Methods in Engineering 38 (1995) 549–564.
- M. Kobayashi, N. Ohno, Implementation of cyclic plasticity models based on a general form of kinematic hardening, International Journal for Numerical Methods in Engineering 53 (2002) 2217–2238.
- J. Clausen, L. Damkilde, L. Andersen, Efficient return algorithms for associated plasticity with multiple yield planes, International Journal for Numerical Methods in Engineering 66 (2006) 1036–1059.
- X. Tu, J. E. Andrade, Q. Chen, Return mapping for nonsmooth and multiscale elastoplasticity, Computer Methods in Applied Mechanics and Engineering 198 (2009) 2286–2296.
- W. M. Coombs, R. S. Crouch, C. E. Augarde, Reuleaux plasticity: Analytical backward euler stress integration and consistent tangent, Computer Methods in Applied Mechanics and Engineering 199 (2010) 1733–1743.
- T. Grilo, R. Valente, R. de Sousa, Assessment on the performance of distinct stress integration algorithms for complex non-quadratic anisotropic yield criteria, International Journal of Material Forming 7 (2014) 233–247.
- L. Szabó, A semi-analytical integration method for J2 flow theory of plasticity with linear isotropic hardening, Computer Methods in Applied Mechanics and Engineering 198 (2009) 2151–2166.
- A. Kossa, L. Szabó, Exact integration of the von Mises elastoplasticity model with combined linear isotropic-kinematic hardening, International Journal of Plasticity 25 (2009) 1083–1106.
- L. Szabó, A. Kossa, A new exact integration method for the Drucker-Prager elastoplastic model with linear isotropic hardening, International Journal of Solids and Structures 49 (2012) 170–190.
- M. Rezaiee-Pajand, M. Sharifian, A novel formulation for integrating nonlinear kinematic hardening Drucker-Prager’s yield condition, European Journal of Mechanics -A/Solids 31 (2012) 163–178.
- M. Rezaiee-Pajand, M. Sharifian, M. Sharifian, Angles based integration for generalized non-linear plasticity model, International Journal of Mechanical Sciences 87 (2014) 241–257.
- M. Wallin, M. Ristinmaa, An alternative method for the integration of continuum damage evolution laws, Computational Mechanics 41 (2008) 347–359.
- H.-K. Hong, C.-S. Liu, Lorentz group SOo(5, 1) for perfect elastoplasticity with large deformation and a consistency numerical scheme, International Journal of Non-Linear Mechanics 34 (1999) 1113–1130.
- H.-K. Hong, C.-S. Liu, Internal symmetry in the constitutive model of perfect elastoplasticity, International Journal of Non-Linear Mechanics 35 (2000) 447–466.
- H.-K. Hong, C.-S. Liu, Some physical models with Minkowski spacetime structure and Lorentz group symmetry, International Journal of Non-Linear Mechanics 36 (2001) 1075–1084.
- C.-S. Liu, H.-K. Hong, Using comparison theorem to compare corotational stress rates in the model of perfect elastoplasticity, International Journal of Solids and Structures 38 (2001) 2969–2987.
- C.-S. Liu, Lie symmetries of finite strain elastic-perfectly plastic models and exactly consistent schemes for numerical integrations, International Journal of Solids and Structures 41 (2004) 1823–1853.
- H.-K. Hong, C.-S. Liu, Internal symmetry in bilinear elastoplasticity, International Journal of Non-Linear Mechanics 34 (1999) 279–288.
- C.-S. Liu, C.-F. Li, Geometrical numerical algorithms for a plasticity model with Armstrong-Frederick kinematic hardening rule under strain and stress controls, International Journal for Numerical Methods in Engineering 63 (2005) 1396–1423.
- C.-S. Liu, Computational applications of the Poincaré group on the elastoplasticity with kinematic hardening, Computer Modeling in Engineering and Sciences 8 (2005) 231–258.
- C.-S. Liu, Symmetry groups and the pseudo-Riemann spacetimes for mixed-hardening elastoplasticity, International Journal of Solids and Structures 40 (2003) 251–269.
- C.-S. Liu, A consistent numerical scheme for the von Mises mixed-hardening constitutive equations, International Journal of Plasticity 20 (2004) 663–704.
- C.-S. Liu, Internal symmetry groups for the Drucker-Prager material model of plasticity and numerical integrating methods, International Journal of Solids and Structures 41 (2004) 3771–3791.
- C.-S. Liu, C.-W. Chang, Non-canonical Minkowski and pseudo-Riemann frames of plasticity models with anisotropic quadratic yield criteria, International Journal of Solids and Structures 42 (2005) 2851–2882.
- E. Artioli, F. Auricchio, L. Beirão da Veiga, Integration schemes for von-Mises plasticity models based on exponential maps: numerical investigations and theoretical considerations, International Journal for Numerical Methods in Engineering 64 (2005) 1133–1165.
- E. Artioli, F. Auricchio, L. Beirão da Veiga, A novel optimal exponential-based integration algorithm for von-Mises plasticity with linear hardening: Theoretical analysis on yield consistency, accuracy, convergence and numerical investigations, International Journal for Numerical Methods in Engineering 67 (2006) 449–498.
- E. Artioli, F. Auricchio, L. Beirão da Veiga, Second-order accurate integration algorithms for von-Mises plasticity with a nonlinear kinematic hardening mechanism, Computer Methods in Applied Mechanics and Engineering 196 (2007) 1827–1846.
- M. Rezaiee-Pajand, C. Nasirai, M. Sharifian, Application of exponential-based methods in integrating the constitutive equations with multicomponent nonlinear kinematic hardening, Journal of Engineering Mechanics 136 (2010) 1502–1518.
- M. Rezaiee-Pajand, C. Nasirai, Accurate integration scheme for von-Mises plasticity with mixed-hardening based on exponential maps, Engineering Computations 24 (2007) 608–635.
- M. Rezaiee-Pajand, C. Nasirai, On the integration schemes for Drucker-Prager’s elastoplastic models based on exponential maps, International Journal for Numerical Methods in Engineering 74 (2008) 799–826.
- M. Rezaiee-Pajand, M. Sharifian, M. Sharifian, Accurate and approximate integrations of Drucker-Prager plasticity with linear isotropic and kinematic hardening, European Journal of Mechanics -A/Solids 30 (2011) 345–361.
- M. Rezaiee-Pajand, C. Nasirai, M. Sharifian, Integration of nonlinear mixed hardening models, Multidiscipline Modeling in Materials and Structures 7 (2011) 266–305.
- M. Rezaiee-Pajand, F. Auricchio, M. Sharifian, M. Sharifian, Computational plasticity of mixed hardening pressure-dependency constitutive equations, Acta Mechanica 225 (2014) 1699–1733.
- Z.-N. Yin, H. Xiao, Automatic consistency integrations for the stress update of J2 elastoplastic rate constitutive equations with combined hardening, International Journal for Numerical Methods in Engineering 98 (2014) 590–611.
- M. Rezaiee-Pajand, F. Auricchio, M. Sharifian, M. Sharifian, Exponential-based integration for Bigoni-Piccolroaz plasticity model, European Journal of Mechanics -A/Solids 51 (2015) 107–122.
 |
|
|